Aivory
[원자력기사 실기] 17년 해설 (1 ~ 5번) 본문
※ 공부하는 수험생 입장에서 원자력기사에 관한 문제 해설조차 없는게 안타까워 만들었습니다.
저도 공부하는 입장이라 잘 모르는 부분이 많습니다.
애매한 부분은 빨간색으로 표시했으니, 참고하시면 좋을 것 같습니다.
강조하고 싶은 부분은 형광색으로 표시했습니다.
혹 잘못된 부분, 더 좋은 풀이를 알고 계신 분들은 댓글로 남겨주세요.
원자력기사 실기, 필답형 필승전략, 기출모음
기사시험의 '꽃'이라고 한다면 단연 필답형 시험이라고 할 수 있다. 아무리 필기시험이 어렵다 한들 정답은 4개의 선지 안에 무조건 존재하게 되어있다. 고로 정 모른다면 찍어도 25% 확률로 얻어
nukidiot.tistory.com
모든 문제는 위의 블로그 게시글에서 가져왔음을 밝힙니다.
본 게시글은 PC에 최적화되어 있습니다.
실기는 기본적으로 생각을 적는 것이 많습니다.
이 점 꼭 유의하시고 읽어주시기 바랍니다.
다른 실기 해설들은 https://aivory.tistory.com/72 에서 찾을 수 있습니다.
카카오 화재때문에 며칠간 티스토리에 제대로 접속할 수 없어져서 조금 늦었습니다.
1. 에너지보상형 GM계수관
GM계수관은 자외선이나 가시광선 등에 의한 전자사태(Avalanche)를 최대한 허용하는 방식입니다.
방사선의 종류나 에너지에 관계없이 동일한 크기의 높은 출력펄스를 발생시킵니다.
따라서 단순히 카운트만 계수하는 것이 가능하고 에너지에 대한 정보는 파악하기 어렵습니다.
그러나 검출기 외벽 등에 적절히 차폐를 하게 된다면 낮은 에너지에 대해서는 감쇠가 일어나면서
일정 영역에서의 반응도를 일정하게 만들어 선량을 근사적으로 얻을 수 있습니다.
이를 보상형 GM 계수관이라고 합니다.
2. 스테인리스강의 장단점

3. COLSS 노심운전제한치를 감시하는 변수
COLSS(Core Operating Limit Supervisory System)

아마 이게 맞을 겁니다.
1. 노심 출력
2. 노심 출력 분배
3. MDNBR 여유도
4. 선형열비율제한여유도
5. 노심방위출력기울기도
4, 5번은 우리말로 해석이 조금 어색하네요.
4. 흡수선량 계산
흡수선량 계산 문제입니다.
조건은 다음과 같습니다.
$$ \Gamma = 0.5 [ \cfrac{ R \cdot m^{2} } {h \cdot Ci} ], r = 2[m], A = 2[Ci] $$
$$ 1.173[MeV], 1.332[MeV] ~per~ Decay$$
붕괴당 1.173, 1,33 두 개를 방출하는걸 보니 Co60인것 같네요.
$$ \dot{X} = \frac{\Gamma A}{r^2} $$
$$ \therefore \dot{X} = \frac{ 0.5 \times 2 }{2^2} = 0.25 [R/h] $$
조금 헷갈리는게 붕괴당 두 개의 감마선을 방출하므로 2를 곱해주냐 마느냐 입니다.
아마 해주지 않을 것 같긴 한데..
이 부분은 추후 추가하도록 하겠습니다.
5. 흡수선량 계산
$$ \Gamma = 3.3 [ \cfrac{ R \cdot m^{2} } {h \cdot Ci} ] $$
길이 3m, 균일하게 분포한 선 선원으로부터 거리 1m, 각도 100°
미리 말씀드리자면, 이 문제의 정확한 답은 못 구했습니다.
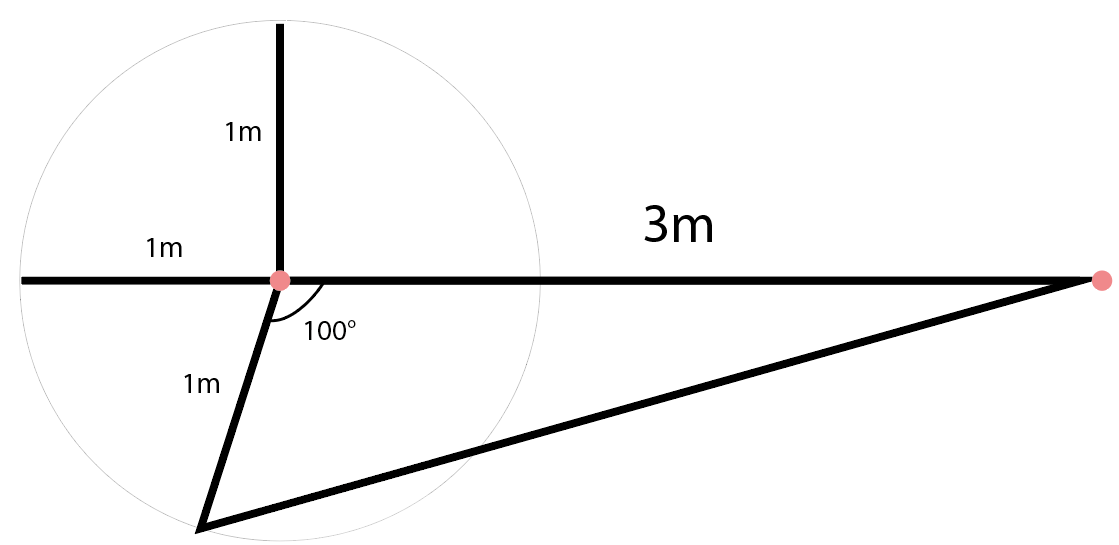
문제의 조건이 조금 애매하긴한데 설명대로라면 위와 같은 그림이 될 것입니다.
즉, 아래의 빨간 점에서의 선량을 구하는 것이 목표입니다.
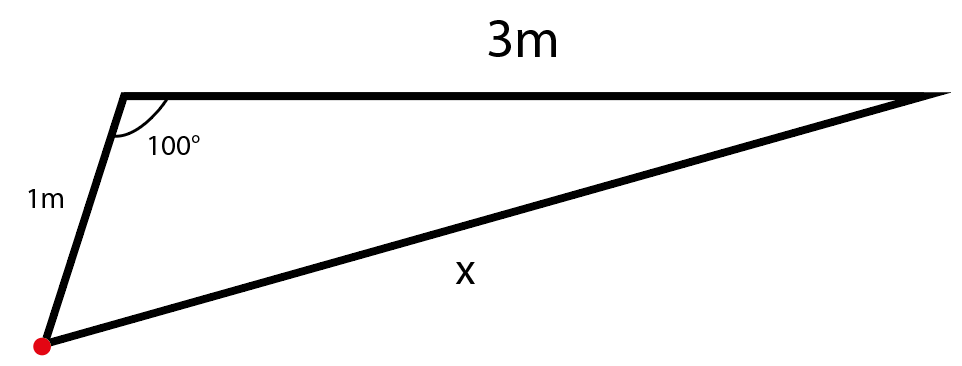
공식에 따르면 흡수선량을 구하기 위해서는 감마상수, 방사능, 거리가 필요합니다.
방사능은 문제 조건에서 제시되지 않았기 때문에, 계산의 편의를 위해서 1Ci로 가정하겠습니다.
즉, 3m라는 직선에 무한히 많은 점이 있는데 그 점 하나하나가 다 1Ci라는 뜻입니다.
(이 부분도 올바른 가정인지 잘 모르겠네요.)
그러면 이제 거리 x를 구해야합니다.
지금 두 변의 길이와 그 사이의 각도를 알고 있으므로 코사인 법칙을 이용할 수 있습니다.
코사인 법칙 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 기하학에서 코사인 법칙(cosine法則, 영어: law of cosines)은 삼각형의 세 변과 한 각의 코사인 사이에 성립하는 정리이다. 이에 따르면, 삼각형의 두 변의 제곱합에
ko.wikipedia.org
$$ x^{2} = 1^{2} + 3^{2} + cos(100^{\circ}), ~~\therefore x = 3.323[m] $$
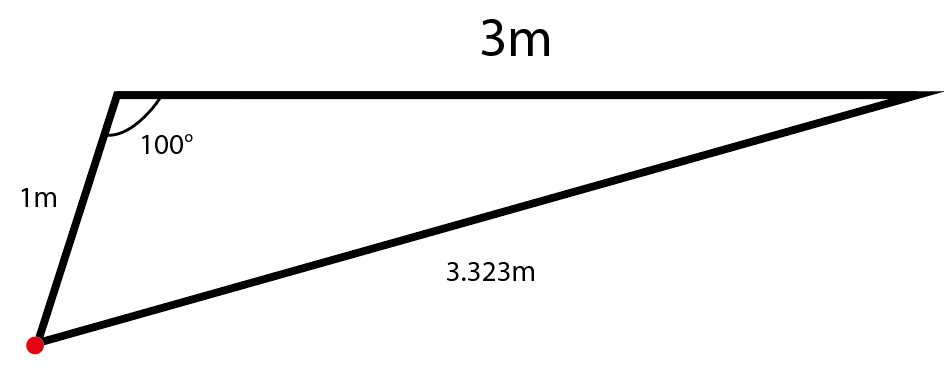
이제 적분을 통해 값을 구할 수 있습니다.
거리는 1부터 3.323까지이므로
\[ \int_{1}^{3.323} \cfrac{ \Gamma A}{ r^2 } \,dr \approx 2.33 \]
계산해주면 2.33 정도가 나옵니다.
이 값이 말이 안되는게
당장에 1m 일때는 3.3이 나오고
3.323m 일 때는 0.3정도가 나옵니다.
둘 만 더해줘도 3.6이 넘어가는데...
개인적인 생각으로는
\[ \int_{1}^{3.323} \Gamma A r^2 \,dr \approx 39.5 \]
아마 이 정도는 되어야 하지 않을까... 싶네요
아무튼 이 부분도 추후 추가하도록 하겠습니다.
'원자력기사(실기) > 실기 기출 해설' 카테고리의 다른 글
| [원자력기사 실기] 17년 해설 (11 ~ 14번) (0) | 2022.10.20 |
|---|---|
| [원자력기사 실기] 17년 해설 (6 ~ 10번) (0) | 2022.10.19 |
| [원자력기사 실기] 18년 해설 (9 ~ 12번) (1) | 2022.10.15 |
| [원자력기사 실기] 18년 해설 (5 ~ 8번) (1) | 2022.10.15 |
| [원자력기사 실기] 18년 해설 (1 ~ 4번) (0) | 2022.10.14 |




