[원자력기사] 22년 86번 해설

※ 공부하는 수험생 입장에서 원자력기사에 관한 문제 해설조차 없는게 안타까워 만들었습니다.

저도 공부하는 입장이라 잘 모르는 부분이 많습니다.

애매한 부분은 빨간색으로 표시했으니, 참고하시면 좋을 것 같습니다.

강조하고 싶은 부분은 형광색으로 표시했습니다.

혹 잘못된 부분, 더 좋은 풀이를 알고 계신 분들은 댓글로 남겨주세요.

 

https://www.comcbt.com/

최강 자격증 기출문제 전자문제집 CBT

모든 문제는 이 곳에서 다운 및 열람할 수 있습니다.

본 게시글은 PC에 최적화되어 있습니다.

 

다른 해설들은 https://aivory.tistory.com/27 에서 찾을 수 있습니다.

 

 

 

정답 : 4

 

22년 원자력기사의 킬러문제가 아니었을까 싶습니다.

 

저도 나머지 찍을 거 다 찍고 한 10분정도 풀었는데 도저히 안풀려서 그냥 찍고 나왔습니다.

 

천천히 다시 풀어보니까 한 시간정도 걸렸던 것 같네요.

 

 

문제 조건을 천천히 살펴보겠습니다.

 

1시간 동안 공기 시료를 채취 -> 그 후 30분부터 계측을 시작 -> 1시간 계측하니 3600Counts

 

이를 시간에 따른 방사능에 대한 그래프로 그려보면 다음과 같습니다.

 

 

Ar-41의 반감기가 1.83시간으로 주어졌습니다.

 

반감기가 굉장히 짧기 때문에 방사능을 포집하면서 동시에 붕괴가 일어나게됩니다.

 

따라서 한 시간동안 포집을 하더라도 선형적으로 증가하지 않고 지수적으로, 수렴 값에 다가가며 증가합니다.

 

그리고 한 시간 이후 부터는 더 이상의 포집은 없고 붕괴만 합니다.

 

따라서, 지수적으로 감소할 것입니다.

 

 

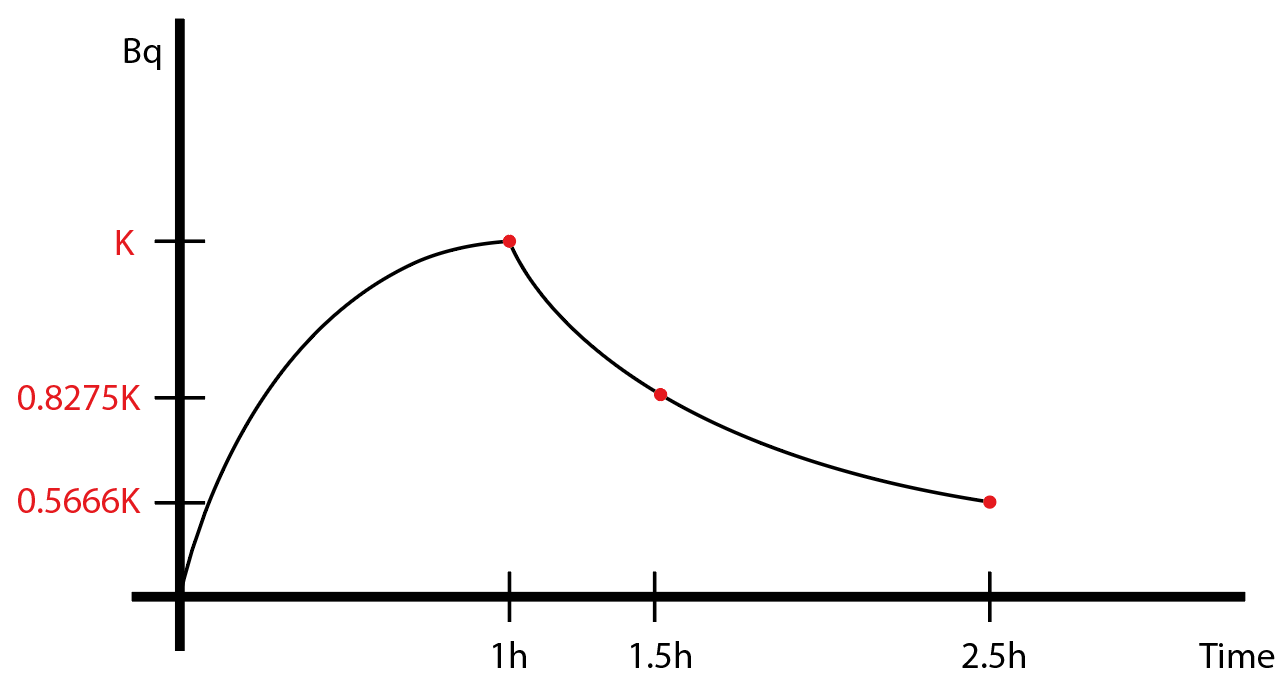
1시간 일때의 방사능을 K[Bq]라고 하겠습니다.

 

그러면 1.5시간에는 0.8275K, 2.5시간에는 0.5666K가 될 것입니다.

 

$$ K \times e ^{ - \frac{ln2}{1.83} \times 0.5 } = 0.8275K $$

$$ K \times e ^{ - \frac{ln2}{1.83} \times 1.5 } = 0.5666K $$

 

 

문제에서 제시한 최종 방사능은 1시간당 3600counts 입니다. 계측 효율은 20% 입니다.

 

따라서,

 

$$ \frac{3600}{0.2} = 18000[counts/hour] = 5[counts/sec] = 5[Bq] $$

 

한 시간에 18000카운트는 결국 초당 5번(5Bq)이라는 말과 같습니다.

 

그리고 3L/min의 속도로 1시간동안 포집을 했으므로

 

$$ 3[L/min] \times 60 = 180[L/hour] = 0.18[m^{3}/hour] $$

 

한 시간에 0.18[m^3] 만큼 포집했습니다.

 

$$ \frac{ 5[Bq] }{ 0.18[m^{3}] } = \frac{ 27.78[Bq] }{ 1[m^{3}] } $$

 

(1m^3으로 환산하면 27.78)

 

 

 

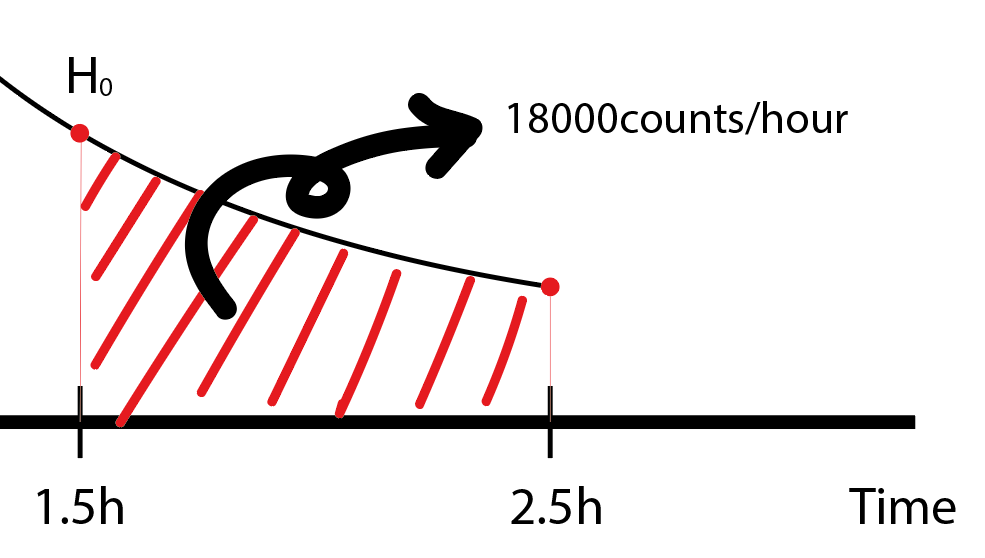
그래프를 조금 더 자세히 살펴보겠습니다.

 

18000counts/hour은 다시 말하면

 

한 시간동안 쭉 포집했더니 18000counts가 되었다는 뜻입니다.

 

즉, 위의 그래프에 빗금친 영역을 전부 더해주니 18000counts가 나왔다는 말입니다.

 

 

 

이렇게 생각해볼까요?

 

반감기가 무척 긴 핵종을 측정했다고 하면

 

방사능 그래프가 거의 일직선일 것입니다. 반감기가 기니까요.

 

한 시간을 포집한다고 가정한다면 지금의 방사능이나 한 시간 후의 방사능이나 거의 비슷할 것입니다.

 

만약 지금 초당 10번 count 된다면, 30분 후도, 1시간 후도 초당 10번일테니

 

10 * 3600 = 36000count가 되겠죠.

 

그러나 이 문제의 경우는 다릅니다.

 

반감기가 짧기 때문에 지금의 count와 한 시간 후의 count에 차이가 있을 수 밖에 없습니다.

 

이를 구하기 위해 적분을 사용하는 것이고요.

 

 

 

1.5시간일 때의 값을 H0라고 잡으면 적분을 통해 H0을 구할 수 있습니다.

 

(한 시간 적분이므로(1.5h -> 2.5h) 0 -> 1로 정적분)

 

$$ H_{0} \times \int_{0}^{1} e^{ -\lambda t} dt = H_{0} \times \frac{1 - e ^{ - \frac{ln2}{1.83} } }{ \frac{ln2}{1.83} } =18000 $$

 

$$ \therefore H_{0} = \frac{ 6[Bq] }{ 0.18[m^{3}] } $$

 

즉, 1.5시간일 때 위와 같은 결과를 갖습니다.

 

$$ H_{0} = 0.8275K $$

 

$$ \therefore K = \frac{H_{0}}{0.8275} = \frac{7.25[Bq]}{0.18[m^{3}]} = 40.3[Bq/m^{3}] $$

 

이제 다 왔습니다.

 

 

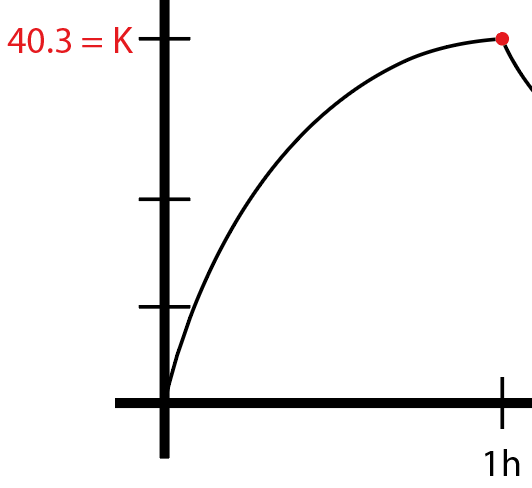
1시간 일 때 40.3 이므로 초기값을 구하기 위해서 역시 적분을 사용해주면 됩니다.

 

초기값을 x로 둔다면

 

$$ x \times \int_{0}^{1} e^{ -\lambda t} dt = 40.3 $$

$$ x \times \frac{ 1 - e^{ - \frac{ln2}{1.83} }    }{  \frac{ln2}{1.83} } = 40.3 $$

$$ \therefore x = 48.4 [Bq/m^{3}] $$

 

사실 저도 올바른 풀이 과정을 알고 푼 것은 절대 아닙니다.

그냥 조건에 맞춰 이 식 저 식 대입해보니 값이 나왔을 뿐입니다.

다시 풀라고 하면 좀 힘들 것... 같기도 하고..

이해가 잘 되셨을지 잘 모르겠네요.

 

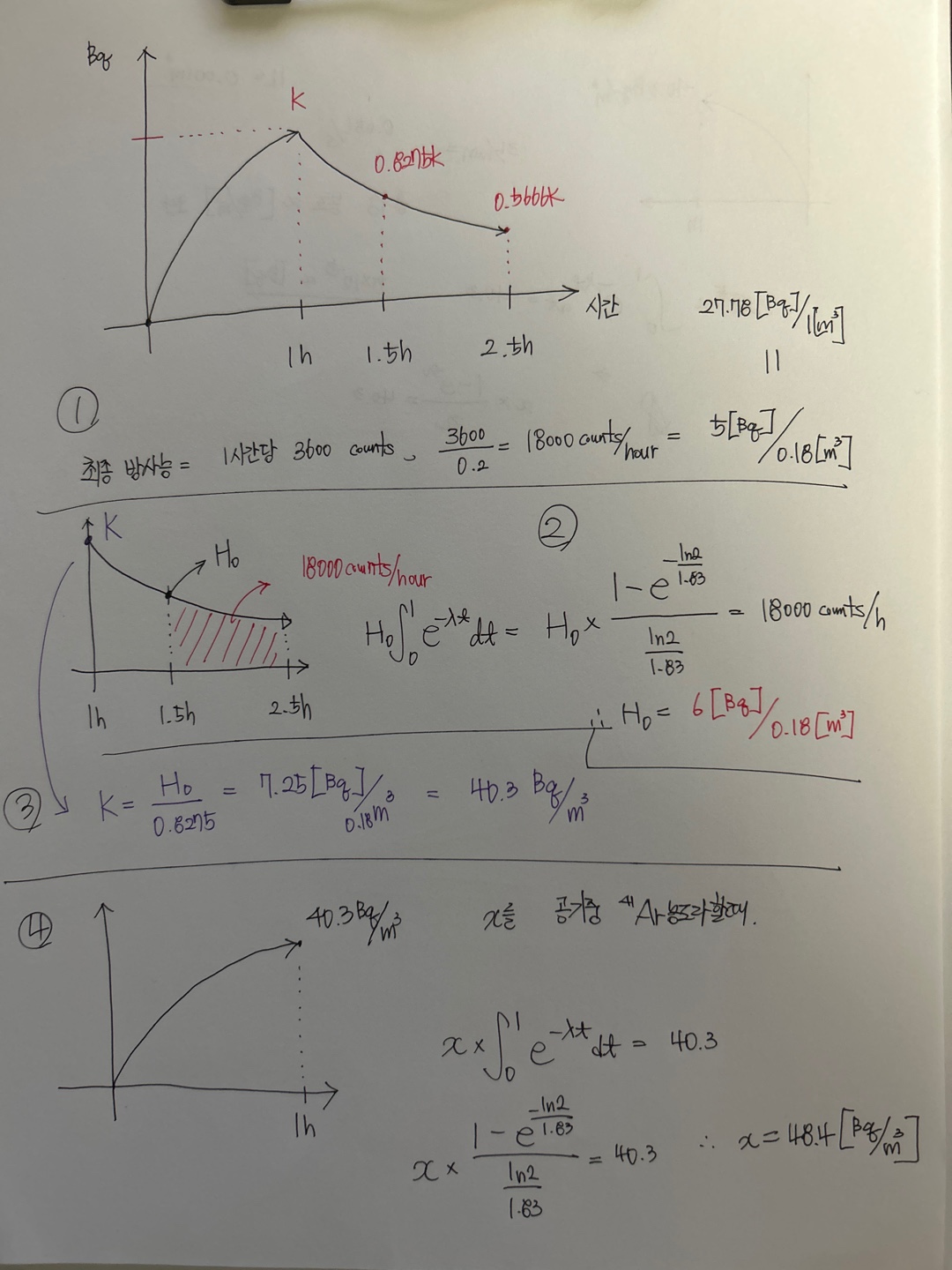
문제 풀이 과정을 정리한 식을 첨부합니다.